CONVERGÊNCIA GLOBAL DE UMA REDE NEURAL DINÂMICA NA OTIMIZAÇÃO DE UM MODELO LINEAR

GLOBAL CONVERGENCE OF A DYNAMIC NEURAL NETWORK IN OPTIMIZATION OF A LINEAR MODEL

CONVERGENCIA GLOBAL DE UNA RED NEURONAL DINÁMICO EN OPTIMIZACIÓN DE UN MODELO LINEAL

Walter Roberto Vergara¹ (waltervergara@ufgd.edu.br)
Fabio Alves Barbosa² (fabiobarbosa@ufgd.edu.br)
Rone Vieira Oliveira³ (rone.vieira.oliveira@hotmail.com)

^1,2,3 Universidade Federal da Grande Dourados - UFGD
Faculdade de Engenharia, Curso de Engenharia de Produção/FAEN

Resumo

Um método é apresentado baseado nos multiplicadores de Lagrange Aumentados no gradiente da rede neural de Hopfield (MLAH). Um problema de programação inteira é transformado em outro problema equivalente substituindo as restrições zero-um por restrições com igualdade quadráticas e côncavas. Esse problema é resolvido utilizando o Lagrangeano Aumentado e a técnica de Hopfield. O método MLAH é comparado com o método de Branch and Bound em termos de valores objetivos otimizados. Os multiplicadores de Lagrange em nosso método fornecem a força de orientar a pesquisa ao ponto mínimo global. Este ponto é movido na direção fornecida pelos multiplicadores de Lagrange. Resultados experimentais são apresentados.

Palavras-chave: Pesquisa Operacional, Otimização, Método dos Multiplicadores de Lagrange, Programação Inteira, Redes Neurais.

Abstract

A method is presented based on Lagrange multipliers Increased the gradient of the Hopfield neural network (MLAH). An integer programming problem is transformed into an equivalent problem by replacing the zero-one restrictions for restrictions and concave quadratic equality. This problem is solved using the Augmented Lagrangian technique and Hopfield. The method MLAH is compared with the method of Branch and Bound optimized in terms of objective values. Lagrange multipliers in our method provide the force to guide the search to the global minimum point. This point is moved in the direction provided by the Lagrange multipliers. Experimental results are presented.

Keywords: Operational Research, Optimization, Method of Lagrange Multipliers, Integer Programming, Neural Networks.

Resumen

Se presenta un método basado en los multiplicadores de Lagrange Aumento de la pendiente de la red neuronal Hopfield (Mlah). Un problema de programación entera se transforma en un problema equivalente al reemplazar las restricciones cero-uno para las restricciones y la igualdad cuadrática cóncava. Este problema se resuelve utilizando la técnica aumentada de Lagrange y de Hopfield. El método Mlah se compara con el método de Branch y Bound optimizado en términos de valores objetivos. Multiplicadores de Lagrange en nuestro método proporciona la fuerza para guiar la búsqueda hasta el punto mínimo global. Este punto se mueve en la dirección proporcionada por los multiplicadores de Lagrange. Se presentan resultados experimentales.

Palabras clave: Investigación Operativa, Optimización, Método de los Multiplicadores de Lagrange, Programación Entera, Redes Neuronales.

 

Introdução

Uma das ideias computacionais mais úteis dos anos 70 é a observação que muitos problemas difíceis podem ser vistos como problemas fáceis, quando relativamente reduzimos o número de restrições. Elas podem ser eliminadas depois de inseridas na função objetivo de um vetor de multiplicadores, chamados de multiplicadores de Lagrange, produzindo outro problema equivalente denominado Lagrangeano, fácil de resolver e a solução ótima esta no limite inferior (para problemas de minimização) do valor ótimo no problema original.

Considere o seguinte problema de otimização:
Minimize f(x, y), ou seja, desejamos encontrar o ponto mínimo desta função, sujeito a g(x, y) = c.

O método introduz uma variável λ, chamada de multiplicador de Lagrange. A partir disso, a função de Lagrange é definida assim:

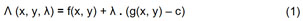
Nesta função, o termo λ pode ser adicionado ou subtraído. Se f(x, y) é um ponto de mínimo para o problema original, então existe um λ tal que (x, y, λ) é um ponto estacionário para a função lagrangiana, ou seja, existe um ponto para o qual as derivadas parciais de Λ são iguais a zero e, como todos os pontos estacionários não permitem uma solução para o problema original, o método dos multiplicadores de Lagrange é uma condição necessária que garante uma solução para problema de otimização com restrições.

Assim, o problema Lagrangeano pode ser transformado em outro problema de Relaxação Linear na qual os limites da solução ótima encontram-se em um algoritmo de busca do tipo Branch and Bound (LAMPERT, et al., 2004; SOMOL, et al., 2004). Além disso, no limite inferior do vetor solução, é possível estimar quão próxima estará a solução viável disponível na solução ótima. Também, podemos verificar que a abordagem da relaxação Lagrangeana oferece um número de vantagens importantes sobre a programação linear (ANDREANI, et al., 2008; WEN, et al., 2010).

Vários pesquisadores já representaram o problema de otimização linear como uma estrutura de rede neural na qual as atribuições são representadas pela ativação dos nós e as restrições pelas conexões, possivelmente com diferentes pesos (HOPFIELD, 1984; XIA; WANG, 2004; ANDREANI, et al., 2005). Ele foi representado como um problema dinâmico através de um circuito elétrico analógico no qual os amplificadores operacionais são considerados como os neurônios.

Embora exista uma série de pesquisas, antes do ano 2000, sobre modelos de redes neurais em conjunto com os multiplicadores de Lagrange dinâmicos, tanto em problemas teóricos quanto práticos, as pesquisas de Wacholder et al. (1989) e Liao et al. (1999) são fundamentais na resolução de sistemas com restrições lineares por meio de redes neurais.

Nesta pesquisa consideramos o problema de encontrar o ponto mínimo global de uma função do problema generalizado de atribuição e demonstramos de forma teórica e numérica que modelos de redes neurais têm um melhor desempenho que métodos tradicionais na solução de problemas. Para atingir nosso objetivo definimos e analisamos uma espécie de estrutura de rede neural, baseada na função dos multiplicadores de Lagrange. Geralmente, esta abordagem é desenvolvida em três passos. Primeiro, as restrições de um problema de otimização são relaxadas em outro problema equivalente de otimização sem restrições, isto é, as restrições zero-um são substituídas por restrições de igualdade quadráticas côncavas com o objetivo de forçar as variáveis de decisão a ser zero ou um. Segundo, a partir do problema de otimização sem restrições, um conjunto de equações diferenciais é derivado. Terceiro, de acordo com o sistema dinâmico é implementado um vetor neural de camada interativa (CICHOCKI; UNBEHAUEN, 1992).

 

1 A Natureza do Problema

Em um problema de atribuição de carga deve-se maximizar o benefício ao se atribuir n trabalhos a m agentes, n > m, de tal forma que cada trabalho seja atribuído a apenas um único agente. Levando-se em conta as restrições de capacidade de cada agente

cuja variável x é requerida para satisfazer as restrições de igualdade

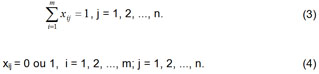
e as restrições de desigualdade linear

• xij é a variável de decisão zero-um, que assume o valor de 1 quando existe uma atribuição do i-ésimo elemento ao j-ésimo elemento e zero em outro caso, i = 1, 2, ..., m; j = 1, 2, ..., n.
• Cada elemento (j) somente pode ser servido por um elemento (i) (restrição 3).
• O total de carga de cada centro de serviço não deve exceder sua capacidade (restrição 4).

Esse problema pode ser considerado como um problema de multimochilas, se considerarmos todos os centros de serviços como mochilas e os consumidores como os objetos. A seguir discutimos e implementamos um modelo de rede neural a esse tipo de problema.

 

2 Método para minimizar o problema de atribuição

Uma técnica bem conhecida para resolver o problema de programação inteira (Equação 2-5), isto é, a minimização de um problema de otimização discreta com restrições, é a utilização da função de Lagrange Aumentado. Este método de otimização baseado em subgradientes utiliza uma matriz de multiplicadores de Lagrange sobre os dados (Equação 6). Na aplicação do método é assumido que o problema é viável e que o conjunto de soluções viáveis de cada restrição relaxada obtida do modelo é um conjunto finito.

A seguinte função de Lagrange de mxn variáveis é utilizada para tal propósito.

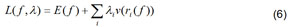
onde i > 0 são os multiplicadores estimados de Lagrange e onde ri(x) = aTx – bi representam os resíduos e v(ri(x)) = Max{0, sgn(ri(x) P(ri(x))} são as funções de penalidade P(ri(x))  0.

A função L(u) é côncava e linear de forma que todo ótimo local é também um ótimo global. Ainda mais, esta função facilita a aplicação do método dos gradientes para resolver o problema (Equação 2-5). Como essa função não é diferenciável em qualquer parte, os métodos clássicos de programação não-linear, como por exemplo, método do gradiente, método do gradiente conjugado, etc., não podem ser aplicados a ela. Então, podemos generalizar os métodos clássicos dos gradientes tomando, em cada passo, a direção do gradiente, se a função é diferenciável no ponto u ou qualquer subgradiente g(x)  L(u) se L não é diferenciável em u.

Para encontrar um estado da função denominado “mínimo local” sujeito a certas restrições é necessário que sejam pontos estacionários na função de Lagrange:

Se é um ponto máximo global na qual se cumpre que

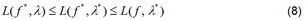
então, é um mínimo local de E(f) que satisfaz (GRIVA, et al., 2009).

Os termos finitos considerados na função de penalidade quadrática,

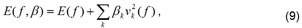
podem ser adicionados à função de Lagrange (Equação 6), transformando essa expressão em outra função denominada de Lagrangeano Aumentado (CICHOCKI e UNBEHAUEN, 1994).

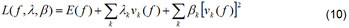
onde os k representam um conjunto de pesos de penalidade finitos. A adição dos termos de penalidade não altera os pontos estacionários do vetor solução e, às vezes, no processamento de dados evita realizarem cálculos oscilatórios sem nenhum objetivo conduzindo-se a convergência da função. Como os fatores de k são finitos, o mau condicionamento de um problema é contornado e aliviado quando k  .

A expressão (Equação 10) determina que a função de energia descenda na função f enquanto sobe nos multiplicadores de Lagrange ().

Uma questão que surge na solução do problema de programação inteira é como tratar as restrições zero-um. Esse caso acontece quando a função solução ( ) é obtida como uma matriz binária, isto é, quando o espaço de soluções contém os limites dos valores das variáveis. Esse problema foi pesquisado por Cichocki e Unbehauen (1994), Agar e Salhi (1998), Wu e Chow (2007), Birgin e Martinez (2008).

Eles propuseram que essas restrições explícitas das variáveis de decisão estivessem relaxadas e dentro da formulação do Lagrangeano Aumentado e, posteriormente manipuladas no processo de minimização do Lagrangeano; isto é, formular uma sequência de problemas (Equação 10) e minimizá-la dentro da região definida pelos limites das variáveis.

Nessa abordagem todas as desigualdades lineares são incorporadas na função Lagrangeano Aumentado. Essa estratégia já foi implementada com sucesso no programa LANCELOT cujo objetivo foi a resolução de problemas de otimização de grande porte (CONN, et al., 1993).

 

3 Abordagem do Modelo de Rede Neural

Muitos pesquisadores têm utilizado o método do gradiente da rede neural de Hopfield para encontrar uma solução ao problema de minimização com restrições (HOPFIELD e TANK, 1985; HOLMBERG, et al., 1999; RONNQVIST, et al., 1999; SEXTON, et al., 2006). Esse esquema foi ilustrado como um modelo de atribuição difusa (ROSENFIELD, et al., 1976), no qual os valores de saída (v) da rede pertencem ao intervalo [0, 1] e representam a força na qual uma classe i é atribuída a uma determinada posição. Cada nó de saída tem uma posição em um hiperplano de quadrante não-negativo de um espaço real multidimensional. Em otimização combinatória, esse método é muito eficiente porque utiliza a projeção do gradiente para escolher a melhor direção e magnitude para o estado envolvido (TRAGANTALERNGSAK, et al., 2000).

Nesta pesquisa introduzimos o método dos multiplicadores de Lagrange no modelo do gradiente da rede neural de Hopfield. Em termos da energia otimizada, o algoritmo se desempenha quase tão bem como no método da simulação annealing, conforme foi mostrado nas pesquisas de Li (1996). O algoritmo deduzido é amplamente distributivo e útil em implementações analógicas.

Consideremos o estado do problema de otimização (Equação 2-5). As restrições zero-um do problema podem ser eliminadas transformando o problema de programação inteira original em outro problema equivalente de programação não-linear, substituindo essas restrições zero-um por restrições igualmente quadráticas côncavas não-lineares da seguinte forma:

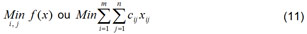
Sujeito às seguintes restrições:

O modelo descrito (Equação 11-14) é equivalente ao problema original de programação inteira zero-um (Equação 2-5).

Na função de Lagrange utilizamos o fator de penalidade com o objetivo de relaxar as restrições lineares de igualdade e desigualdade, e somente os multiplicadores de Lagrange para relaxar as restrições de igualdade da função quadrática côncava não-linear.

O seguinte sistema dinâmico é utilizado para encontrar o ponto mínimo global da função de Lagrange (CICHOCKI; UNBEHAUEN, 1992).

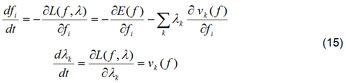
Muitos pesquisadores realizaram experimentos numéricos bem sucedidos na convergência ao ponto mínimo global desse sistema (AGAR e SALHI, 1998; HOLMBERG et al., 1999; ANDREANI, et al., 2005, 2008; WU; CHOW, 2007). Atualmente, esse modelo dinâmico de equações está sendo utilizado em muitas aplicações utilizando as redes neurais como fator de processamento de dados (SEXTON et al., 2006).

Depois que os termos de penalidade (Equação 9) são adicionados à função L (Equação 10), o sistema de equações dinâmico em fi toma a seguinte forma:

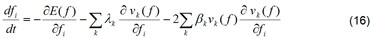
Conforme nossa teoria pesquisada e desenvolvida em relação ao modelo de Lagrange Aumentado, um sistema dinâmico é construído cujo ponto de equilíbrio é o ponto mínimo global da função de Lagrange Aumentado.

Assim, fazendo as respectivas operações e deduções, o problema de otimização em análise pode ser convertido em outro problema equivalente de otimização sem restrições utilizando uma função de penalidade quadrática pelo método da função de Lagrange como segue:

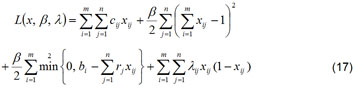
onde é o vetor de multiplicadores de Lagrange.

Segundo Cichocki e Unbehauen (1994), o processamento das redes neurais acontece utilizando um sistema de equações diferenciais ordinárias conforme é representado na Equação 18.

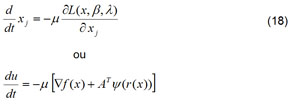
A função de energia do modelo de atribuição generalizado pode ser mapeada por um conjunto de equações diferenciais ordinárias não-lineares, onde os pontos de equilíbrio do sistema dinâmico construído são os pontos do cume da função de Lagrange Aumentada (Equação 15).

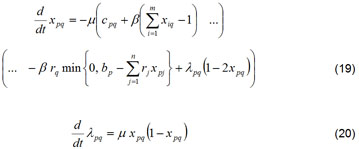
onde é o valor da taxa de aprendizado e p = 1, 2, ..., m; q = 1, 2, ..., n.

O sistema de equações diferenciais deduzidos (Equação 19 e Equação 20) a partir da função de Lagrange aumentado adapta os multiplicadores de Lagrange segundo as restrições de igualdade da função quadrática côncava.

Qualquer estado fi(I)  [0, 1] pode ser representado como uma variável interna e introduzida em xi(I) via

sujeita às seguintes restrições de confiabilidade:

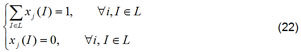
onde g() é a função de transferência, por exemplo, sigmoide,

controlada pelo parâmetro T > 0. A introdução das variáveis à função de energia pode ser considerada como L(u) = L(x(u)). Esse tratamento determina que xi(I)  [0, 1], validando a expressão (4). Um verdadeiro ganho acontece quando T  0+, assim xi(I) é forçado a assumir valores de zero ou um, dependendo se ui(I) é positivo ou negativo, nesse sentido, também se valida à restrição (Equação 4).

No modelo de rede neural (Equação 19-20), o primeiro termo da esquerda da Equação 19 minimiza as conexões entre os nós, enquanto que os outros termos penalizam as configurações não balanceadas. As equações diferenciais não são apresentadas porque as expressões são muito extensas. O funcionamento da estrutura da rede neural pode ser observado na Figura 1.

 

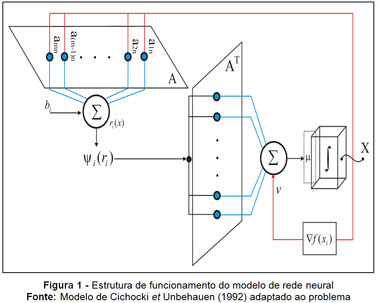
4 Simulação Numérica

A seguir, analisemos o seguinte problema de atribuição de tarefas no desenvolvimento de software por programadores. Uma firma de processamento de dados dispõe de cinco programadores: C1, C2, C3, C4 e C5. Em um determinado dia, existem seis tipos de trabalhos para serem executados (T1 a T6). O custo de processamento de cada um desses trabalhos é diferente em cada um dos programadores. A Tabela 1 resume os custos de desenvolvimento de cada trabalho segundo o programador que eventualmente for designado a executá-lo:

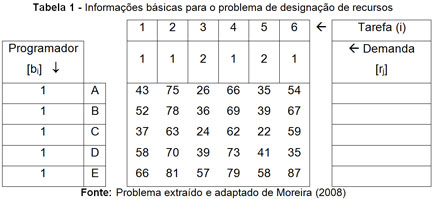
O problema da gerência consiste em designar um programador para cada tipo de trabalho de modo a minimizar o custo total de desenvolvimento dos trabalhos pelos programadores. Quando uma determinada operação é realizada por um operador específico, os problemas são relativamente menores; mas, quando existem diversos operadores aos quais as operações podem ser alocadas, os problemas são maiores. Por isso, nestes tipos de problemas procura-se associar a carga de trabalho a um objetivo principal, por exemplo, diminuir os custos de processamento, minimizar os tempos de processamento do sistema, maximizar os lucros ou a eficiência.

Nossa primeira aproximação ao problema de atribuição de recursos foi realizada pelo método de Branch and Bound (vide SOMOL et al., 2004). Essa técnica nos fornece uma aproximação do valor ótimo da função objetivo. O valor da função de custo (325) representa apenas um critério de solução, e não o custo mínimo para realizar todas as operações. Os resultados das alocações e eliminações são visualizados na Tabela 2.

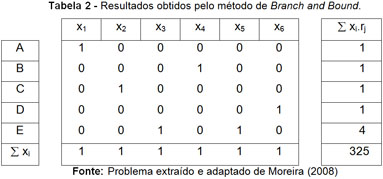
Para verificar o comportamento da rede neural em função dos multiplicadores de Lagrange com o problema generalizado de atribuição, foi usado o conjunto de equações diferenciais ordinárias como foi descrito em (Equação 19 e 20) com o objetivo de obter o mínimo global da função objetivo. As equações diferenciais ordinárias do sistema foram resolvidas numericamente pelo método de Runge-Kutta-Fehlberg de ordem sexta. Os resultados são mostrados na Tabela 3.

Uma das características mais importantes das redes neurais é o processamento de informação incerta, isto é, mesmo que a informação esteja incompleta, afetada por ruído, ainda é possível obter-se estimativas confiáveis apesar de que às vezes os valores apresentem aparentemente tendência de não convergência (CICHOCKI e UNBEHAUEN, 1992). Na rede neural, o próprio algoritmo realiza otimização, encontrando os parâmetros, que são os pesos, que proporcionam o menor erro médio quadrático no mapeamento dos exemplos de treinamento às suas respectivas classes fornecidos.

Por exemplo, os resultados obtidos na Tabela 3 contêm as simulações numéricas computacionais do problema ajustadas a valores inteiros 0 ou 1. Foram realizadas várias simulações com diferentes tipos de taxas de aprendizado (µ) e valores de penalidade (K). Os processos numéricos foram interrompidos em 300 iterações. O resultado numérico do problema pelo método da rede neural dos multiplicadores de Lagrange permite reduzir em mais ou menos três pontos percentuais a função de custo em relação ao método de Branch and Bound. As soluções obtidas usando o modelo neural, variando os parâmetros µ e K, indicam que existe convergência numa melhor solução, apresentando um baixíssimo custo computacional. Portanto, ao ajustar os parâmetros do sistema de equações diferenciais observamos convergência no ponto-solução global. Neste caso, o mínimo local também é o mínimo global em vista que a função objetivo e as restrições foram definidas como côncavas. Na simulação, os valores mais representativos dos experimentos foram com uma taxa de aprendizado de 2 e o valor de penalidade 10.

As junções de técnicas analíticas e de otimização numérica procuram determinar soluções ótimas, principalmente resolvendo sistemas de equações lineares que utilizam derivadas, como por exemplo, o método dos multiplicadores de Lagrange (WU; CHOW, 2007; IZMAILOV; SOLODOV, 2005).

Na avaliação da rede neural, o valor da função objetivo compara a precisão do modelo com os resultados do modelo de referência (Branch and Bound), no qual a predição representa, simplesmente, os valores de todos os padrões de entrada da amostra. Um ajuste é perfeito ou o experimento é representativo quando o valor obtido para a função objetivo é menor que o valor do modelo de referência, e um ajuste pobre ocorre quando ele é maior. As amostras geradas aleatoriamente não são representativas do modelo quando as predições da rede neural não são boas e, em consequência, os valores da função objetivo são não significativos. Todas as simulações foram realizadas em Matlab 10.0®.

 

Considerações Finais

Nesta pesquisa mostramos uma abordagem de transformar as restrições lineares zero-um de um problema generalizado de atribuição em outro problema equivalente com restrições quadráticas côncavas iguais. Uma rede neural é utilizada com o objetivo de resolver o problema de otimização não linear. A rede neural é obtida pela reformulação de um problema de minimização sem restrições por meio de uma função de penalidade.

A rede neural demanda uma grande quantidade de processamento paralelo na solução do problema, assim foi discutido e aplicado o método dos multiplicadores de Lagrange aumentados como forma de obter uma solução rápida, a partir do conjunto de equações diferenciais ordinárias derivados em conjunto com um vetor neural de camada iterativa.

Os testes refletem que, em um problema de otimização combinatória, os multiplicadores de Lagrange inseridos em uma rede neural realizam um bom mapeamento dos objetos em análise (CICHOCKI; UNBEHAUEN, 1994). Essa estrutura permite encontrar o menor caminho entre todos os possíveis, por isso o modelo facilmente fornece soluções locais viáveis.

A metodologia utilizada é consistente e precisa na medida em que integra o conhecimento adquirido pela inter-relação de um número de neurônios dinâmicos. Esse processo iterativo conduz a uma rápida convergência na pesquisa de um ponto mínimo local. A melhoria na otimização dos resultados é evidente em nosso exemplo. De qualquer forma, a redução no tempo de processamento requerido para obter tal precisão não foi dramática.

O seguinte passo de nosso desenvolvimento é o uso desta abordagem na solução de problemas de programação não-linear probabilística e também na resolução de problemas de controle ótimo.

 

Referências

AGAR, M.C.; SALHI, S. Lagrangean Heuristics Applied to a Variety of Large Capacitated Plant Location Problems. The Journal of the Operational Research Society, v.49, n.10, p.1072-1084, 1998.

ANDREANI, R.; BIRGIN, E.G.; MARTINEZ, J.M.; SCHUVERDT, M.L. Augmented Lagrangian methods under the constant positive linear dependence constraint qualification. Mathematical Programming, v.111, n.1-2, p.5-32, 2008.

ANDREANI, R.; BIRGIN, E.G; MARTINEZ, J.M.; SCHUVERDT, M.L. On Augmented Lagrangian Methods with General Lower-Level Constraints. SIAM Journal on Optimization, v.18, n.4, p.1286–1309, 2005.

BIRGIN, E.G.; MARTINEZ, J.M. Improving ultimate convergence of an augmented Lagrangian method. Optimization Methods and Software, v.23, n.2, p.177–195, 2008.

CICHOCKI, A.; UNBEHAUEN, R. Neural networks for computing eigenvalues and eigenvectors, Biological Cybernetics, v.68, p.155-164, 1992.

CICHOCKI, A; UNBEHAUEN, R. Neural Network for optimization and signal processing, Wiley & Sons, Chichester, 1994.

GRIVA, Igor; NASH, Stephen; SOFER, Ariela. Linear and nonlinear optimization. Philadelphia: Society for Industrial and Applied Mathematics, ©2009.

HOLMBERG, Kaj; RONNQVIST, Mikael; YUAN, Di. An exact algorithm for the capacitated facility location problems with single sourcing. European Journal of Operational Research, v.113, n.3, p.544-559, 1999.

HOPFIELD, J.J. Neurons with graded response have collective computational ability. In: Proc. Natl. Acad. Sci., USA 81, p. 3088-3092, 1984.

HOPFIELD, J.J.; TANK, D.W. Neural computation of decisions in optimization problems, Biol. Cybern., v.52, p.141-152, 1985.

IZMAILOV, A.; SOLODOV, M. Otimização: Condições de otimalidade, elementos de análise convexa e de dualidade. Rio de Janeiro: IMPA, 2005, 253 p.

LAMPERT, Christoph H.; BLASCHLKO, Matthew B.; HOFMANN, Thomas. Efficient Subwindow Search: A Branch and Bound Framework for Object Localization. Transaction on Pattern analysis and machine intelligence, v.31, n.12, p.2129-2141, 2004.

LI, S.Z. Robustizing robust M estimation using deterministic annealing. Pattern Recognition, v.29, n.1, p.156-166, 1996.

LIAO, L.Z.; QI, H.A neural network for the linear complementarity problem. Math. Comp ut. Modelling, v.29, n.3, p.9-18, 1999.

MOREIRA, D.A. Administração da Produção e Operações. São Paulo: Pioneira Thomson Learning, 2008.

RONNQVIST, Mikael; TRAGANTALERNGSAK, Suda; HOLT, John. A repeated matching heuristic for the single-source capacitated facility location problem. European Journal of Operational Research, v.116, n.1, p.51–68, 1999.

ROSENFIELD, A.; HUMMEL, R.; ZUCKER, S. Scene labeling by relaxation operations. IEEE Transactions on Systems. Man and Cybernetics, v.6, p.420-433, 1976.

SEXTON, Randall S.; McMURTREY, Shannon; CLEAVENGER, Dean. Knowledge discovery using a neural network simultaneous optimization algorithm on a real world classification problem. European Journal of Operational Research, v.168, n.3, p.1009–1018, 2006.

SOMOL, Petr; PUDIL, Pavel; KITTLER, Josef. Fast Branch & Bound Algorithms for Optimal Feature Selection. Transaction on Pattern analysis and machine intelligence, v.26, n.7, p.900-912, 2004.

TRAGANTALERNGSAK, Suda; HOLT, John; RONNQVIST, Mikael. An exact method for the two-echelon, single-source, capacitated facility location problem. European Journal of Operational Research, v.123, n.3, p.473–489, 2000.

WACHOLDER, E.; HAN, J.; MANN, R.C. A neural network algorithm for the multiple traveling salesman problem. Biological Cybernetics, v.61, p.11-19, 1989.

WEN, Zaiwen; GOLDFARB, Donald; YIN, Wotao. Alternating direction augmented Lagrangian methods for semidefinite programming. Mathematical Programming Computation, v.2, n.3-4, p.203-230, 2010.

WU, Sitao; CHOW, Tommy W. S. Self-Organizing and Self-Evolving Neurons: A New Neural Network for Optimization. IEEE Transaction on neural networks, v.18, n.2, p.385-396, 2007.

XIA, Youshen; WANG, Jun. A general projection neural network for solving monotone variational inequalities and related optimization problems. IEEE Transaction on neural networks, v.15, n.2, p.318–328, 2004.

 

Recebido em 22/08/2014
Aceito em 13/11/2014

 

---

Revista Científica On-line Tecnologia – Gestão – Humanismo - ISSN: 2238-5819
Faculdade de Tecnologia de Guaratinguetá
Revista v.4, n.2 – novembro, 2014