ONDAS DE ELLIOTT: aspectos econômicos e matemáticos envolvidos

ELLIOTT WAVES: economic and mathematical aspects involved

ONDAS DE ELLIOT: aspectos económicos y matemáticos involucrados

Walter Roberto Vergara Correio ¹ (waltervergara@ufgd.edu.br)

¹ Universidade Federal da Grande Dourados

Resumo

Este trabalho discute o estudo, análise e descrição do modelo de comportamento dos investidores no mercado financeiro sob a ótica da teoria econômica e matemática desenvolvida por Ralph Nelson Elliott. A pesquisa possibilita o entendimento do processo de tomada de decisão no mercado financeiro através de informações disponibilizadas por agentes econômicos que, posteriormente, serão as entradas dos modelos matemáticos. Uma análise do Índice Bovespa permitiu uma descrição do comportamento do mercado financeiro brasileiro a partir do Princípio das Ondas de Elliott, complementada por entrevistas com os investidores e revisão da literatura, identificando as heurísticas que são utilizadas pelos investidores econômicos. Os resultados da pesquisa confirmam a presença de Ondas de Elliott em períodos pré-determinados. Posteriormente à identificação dos períodos de ondas, foi realizada uma simulação utilizando o Método de Monte Carlo apoiado pelo aplicativo Crystal Ball da Oracle. A pesquisa constatou que a Simulação de Monte Carlo é uma excelente técnica para auxiliar os investidores e analistas de mercado na verificação da probabilidade de ocorrência dos percentuais de Fibonacci nas transições de ondas.

Palavras-chave: Princípio das Ondas de Elliott; Mercado Financeiro; Método de Monte Carlo.

Abstract

This article discusses the process of study, analysis and description of behavior's model of investors in financial market from the perspective of economics and mathematical theory developed by Ralph Nelson Elliott. The research allows an understanding of decision-making process in financial market through information provided by economic agents that, subsequently, will be the inputs of mathematical models. An analysis of Bovespa Index allowed a description of Brazilian financial market behavior from the Elliott Wave Principle, interviews with investors and literature review, identifying the heuristics which are used by economic investors. The survey results confirm the presence of Elliott Waves in predetermined periods. After identifying the periods of waves, it was performed a simulation using the Monte Carlo Method supported by Oracle Crystal Ball software. The research evidenced that the Monte Carlo Simulation is an excellent technique to assist investors and financial analysts in verifying the occurrence probability of Fibonacci Percentages in wave transitions.

Keywords: Elliott Wave Principle; Financial Market; Monte Carlo Method.

Resumen

En este trabajo se analiza el estudio, el análisis y la descripción del comportamiento de los inversores en el modelo de mercado financiero desde la perspectiva de la teoría económica y las matemáticas desarrolladas por Ralph Nelson Elliott . La investigación proporciona una comprensión del proceso de toma de decisiones en los mercados financieros a través de la información proporcionada por los agentes económicos que más tarde serán las entradas de los modelos matemáticos. Un análisis del índice Bovespa permitió una descripción del comportamiento del mercado financiero brasileño de la onda de Elliott, entrevistas con los inversores y la literatura , la identificación de las heurísticas que se utilizan para los inversores económicos. Los resultados de la encuesta confirman la presencia de la onda de Elliott en períodos predeterminados. Después de la identificación de los períodos de onda, se realizó una simulación usando el método de Monte Carlo compatible con la aplicación de la bola cristalina de Oracle . La encuesta encontró que la simulación de Monte Carlo es una técnica excelente para ayudar a los inversores y analistas en la verificación de la probabilidad de ocurrencia de los porcentajes de Fibonacci de transiciones ondas.

Palabras clave: Onda de Elliott principio; Mercados Financieros; Método de Monte Carlo.

 

Introdução

O mercado financeiro consiste de um conjunto de instituições que oferecem diferentes formas de captação e aplicação de recursos. A fim de aumentar a liquidez e negociabilidade dos títulos, um conjunto de normas é criado para regular as transações (instrumentos financeiros). O universo de atores do mercado é fundamentalmente constituído por dois conjuntos de agentes: poupadores (“necessidade de investir dinheiro”) e captadores (“necessidade de pedir dinheiro emprestado”).

As bolsas de valores são mercados públicos onde se realizam operações de compra e venda de títulos e/ou valores mobiliários em mercado livre e aberto, organizado e fiscalizado pela própria bolsa, pelas sociedades-membros e pelas autoridades competentes (ANDREZO e LIMA, 2007).

Os preços das ações indicam o valor de mercado das empresas listadas na bolsa. O principal objetivo dos investidores é obter o maior retorno possível sobre seu investimento, comprando ações por um determinado valor com a expectativa de obter lucro no futuro. Tal atividade implica fazer previsões sobre o mercado, com o objetivo de auxiliar a tomada de decisões na compra e/ou venda das ações no momento mais adequado.

Alguns estudos mostram que as teorias t existentes em uma certa época, tanto as tradicionais como as modernas, não eram suficientes para explicar o comportamento exato dos mercados financeiros (FERREIRA, SILVA e GUILHERME, 2003). Esta lacuna passou a ser preenchida por estudos e pesquisas nas áreas de psicologia, sociologia e antropologia.

No século XX, o contador Ralph Nelson Elliott observou que alguns fatores da economia, como comportamento de massas de investidores, poderiam ser representados por gráficos sinalizados em padrões. A partir dessa constatação, Elliott desenvolveu uma forma de analisar e predizer o movimento das ações e opções de derivativos do mercado financeiro baseado em comportamentos econômicos e dos investidores. Essa representação baseada em padrões foi denominada “Ondas de Elliott”. Considera que as mudanças de preços no mercado financeiro apresentam um progresso estrutural geométrico na forma de ondas.

Esta pesquisa irá observar e analisar o comportamento do mercado através do desenvolvimento do Princípio das Ondas de Elliott usando o comportamento do índice Bovespa, indicador que mede o desempenho das principais ações do mercado brasileiro negociadas na Bolsa de Valores, Mercadorias e Futuros (BM&F BOVESPA, 2012 e BM&F BOVESPA, 2011).

 

2 Princípios das ondas de Elliott

 

2.1 Considerações Iniciais

Por meio de gráficos pode-se observar que os mercados financeiros se movimentam de acordo com uma progressão estruturada em movimentos definidos. Em 1935, Ralph Nelson Elliott definiu oito tipos de movimentos ou ondas que costumam acontecer durante os “movimentos de subida e descida” de qualquer mercado acionário, como representado na Figura 1.

A base da teoria de Elliott consiste na oscilação dos mercados em movimentos no sentido da tendência, entremeados por movimentos no sentido contrário ao da tendência. A afirmação de Elliott está baseada em um pressuposto da psicologia social, o de que grupos de pessoas têm comportamentos que se tornam mais previsíveis à medida que aumenta o número de pessoas envolvidas.

Este princípio pode representar graficamente como grupos de pessoas se comportam, revelando as oscilações que ocorrem, devido à “psicologia de massas, do estado de pessimismo ao otimismo” e, posteriormente, voltam a um estado natural, criando padrões específicos e mensuráveis.

Segundo a teoria de Elliott, um ciclo padrão de tendência do mercado é formado graficamente por grandes ondas bem definidas, onde cada uma delas é formada por grupos menores que reproduzem o mesmo padrão, conforme exibido na Figura 2.

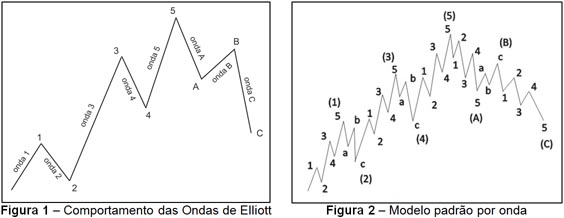
A ideia básica subjacente ao princípio de Elliott é que essas ondas seguem um padrão de crescimento e queda que pode ser analisado segundo os números de Fibonacci.

 

2.2. Sequência de Fibonacci

Elliott encontrou uma forma de medir o ciclo de repetição das ondas, ao relacionar o comportamento do mercado e a sequência de números de Fibonacci (BELMONT, 2010; CALAÇA, 2008; HAYASHI, 2002).

De forma geral, a teoria das ondas de Elliott diz que a razão entre um pico (alta de preços) e um vale (queda dos preços) do gráfico tende a ter um valor aproximadamente igual à razão entre dois números sucessivos da sequência de Fibonacci, como 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144... Elliott estudou a sequência de Fibonacci para tirar conclusões importantes e relacionou esse fato para cinco ondas da seguinte forma: nessa sequência de números, a razão entre um número e o seu antecessor, a partir do quinto termo é um valor próximo a 1,618, que representa o índice de ouro na medição das ondas:

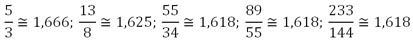
Esses números levam às seguintes considerações:

a) A onda 1 (primeira onda de uma sequência) é a base para se determinar as razões das demais ondas;
b) A onda 2 (segunda onda da sequência) se relaciona com a onda 1, numa razão de 50% a 62% desta;
c) A onda 3 está relacionada à onda 1 segundo a proporção 161,8%, 261,8% ou 423,6%;
d) A onda 4 relaciona-se à onda 3 por uma das relações: 24%, 38% ou 50% desta;
e) A onda 5 está relacionada à onda 1 segundo uma das proporções: 100%, 161,8% ou 261,8%, conforme a Figura 3.

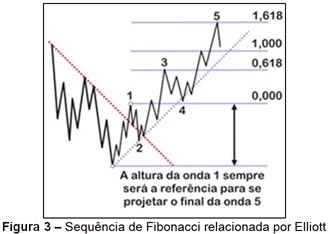
Normalmente encontra-se uma onda que corrija a anterior em uma proporção de aproximadamente 0,62, ou seja, 62% (como apontado nas Figuras 4 e 5), a onda 2 corrige a onda 1 nessa proporção. Por outro lado, a onda 3 transpõe o pico da onda 1, também, em 62%, aproximadamente.

Além disso, nota-se que na representação das ondas se vislumbram outras ocorrências da proporção áurea e de uma razão muito comumente encontrada, conforme Elliott, que é a de 38%: nesse caso, a onda 1 é superada em 62% pela onda 3, a qual é corrigida pela onda 4 em 38%. Assim, a onda 5 é corrigida pela "A" em 62%, aproximadamente.

 

2.3 Relacionamento entre as ondas

Conforme visto anteriormente, as ondas se relacionam entre si através da sequência de Fibonacci. O quantitativo de medição de uma onda é seu tamanho, a distância vertical entre início e final. Essa distância pode ser dada em pontos ou em preço das ações. Desse modo, o tamanho da onda 1 é utilizado para encontrar as razões das ondas 2 e 3, o tamanho da onda 4 pode ser encontrada a partir da onda 3 e a onda 5 apresenta duas relações, uma com a onda 3 e a outra com o início da onda 1 e o final da onda 3.

Segundo Calaça (2008), existem algumas regras básicas para a identificação das ondas impulsivas:

a) A amplitude da onda 3 é sempre a maior de todas as ondas;
b) A amplitude da onda 5 é sempre maior ou igual à amplitude da onda 1;
c) Se a amplitude da onda 3 ou da onda 5 for maior que a da onda 1, a amplitude das mesmas será uma das expansões de Fibonacci;
d) Se a amplitude da onda 3 for maior que a onda 1, então a amplitude da onda 5 é igual a da onda 1;
e) Se a amplitude da onda 5 for maior que a da onda 1, então a amplitude da onda 3 é igual a da onda 1.

 

3 Método de Monte Carlo

 

3.1. Considerações Iniciais

Segundo Vargas (2004), a simulação de Monte Carlo (MC) é um método, na qual a distribuição de resultados é determinada a partir de cálculos sucessivos dos dados analisados, permitindo a construção de diversos cenários. Em cada simulação são utilizados dados aleatórios novos para representar o processo, A combinação dos resultados gera uma distribuição probabilística.

Segundo Silva (2004), a construção de modelos necessita de seleção e análise da interrelação entre as variáveis de entrada que compõem o sistema. A metodologia aplicada neste trabalho para o desenvolvimento do método de simulação de MC foi adaptado do referido autor, conforme os passos a seguir:

a) Determinar as variáveis que participarão da simulação, levando-se em conta a relação entre as mesmas;
b) Determinar a Função de Densidade Probabilística (FDP), das variáveis a serem simuladas, através dos histogramas dos dados históricos;
c) Determinar o número de simulações, considerando um erro determinado;
d) Simular o modelo;
e) Fazer a análise estatística dos dados.

As variáveis abordadas neste trabalho são contínuas e simuladas por variáveis aleatórias caracterizadas pela FDP, o que permite elaborar uma simulação probabilística pelo método de MC.

A FDP, portanto, é a distribuição de probabilidade de uma variável aleatória contínua de uma função matemática que associa o intervalo dos possíveis resultados da variável aleatória. Esta função pode ser estimada através de uma distribuição de frequências (histograma), sendo possível escolher a distribuição que melhor se ajusta à simulação. O conjunto de dados selecionado é agrupado em intervalos e em cada iteração é gerado um valor para as variáveis de entrada.

 

4 Metodologia

A metodologia empregada na realização do presente trabalho incluiu pesquisa bibliográfica que teve como suporte a consulta a fontes diversas, com destaque para livros, entrevistas informais com investidores, analistas de corretoras, revistas e jornais que tratam sobre a economia, bem como artigos recuperados da Internet, que permitem o acesso a dados atualizados sobre a temática em destaque. Assim, é confeccionada uma análise que contempla os eventos que surgem da economia relacionados com a sequência de Fibonacci.

O protocolo de pesquisa foi construído a fim de nortear e garantir que o estudo fosse realizado conforme a metodologia exposta. Assim os procedimentos utilizados para a foram:

a) Definição detalhada dos objetivos da pesquisa;
a) Revisão bibliográfica para compreensão do tema abordado.
b) Coleta de dados;
c) Escolha dos parâmetros utilizando correlação.
d) Identificação dos períodos de onda utilizando planilhas do aplicativo Microsoft Excel;
e) Caracterização dos períodos de ondas utilizando o software Crystal Ball;
f) Simulação de Monte Carlo utilizando o Crystal Ball.

Os dados do índice IBOVESPA foram coletados do sistema Broadcast do site Yahoo! disponível em http://br.finance.yahoo.com, utilizando-se a periodicidade diária. Os dados são fornecidos em planilha eletrônica e constam dos seguintes parâmetros: (a) Data; (b) Valor de abertura; (c) Valor de fechamento; (d) Valor mínimo negociado na data; e (e) Valor máximo negociado na data.

O período selecionado para o experimento foi de 02/09/2002 a 31/09/2012, totalizando uma amostra de 2.508 dados.

Para se aplicar o modelo de simulação do método de MC foi necessário estimar a função de probabilidade para o parâmetro a ser escolhido, sendo que a FDP foi determinada pela análise dos histogramas para cada período de ondas.

As rotinas para a simulação do IBOVESPA e a geração dos números aleatórios foram desenvolvidas no software Microsoft Excel, utilizando, também, o aplicativo Crystal Ball da Oracle.

 

5 Resultados e discussões

 

5.1 Considerações iniciais

Para a identificação dos períodos de ondas foi utilizada uma planilha desenvolvida em Microsoft Excel, que fornece as porcentagens dos números ou grades de Fibonacci, visto que a validação de cada onda é realizada com base neste preceito. A Figura 4 apresenta o gráfico do IBOVESPA obtido a partir do site ADVFN (http://br.advfn.com/), que fornece os gráficos dos pontos de ações, onde se observa o período analisado no presente estudo – 02/09/2002 à 31/09/2012.

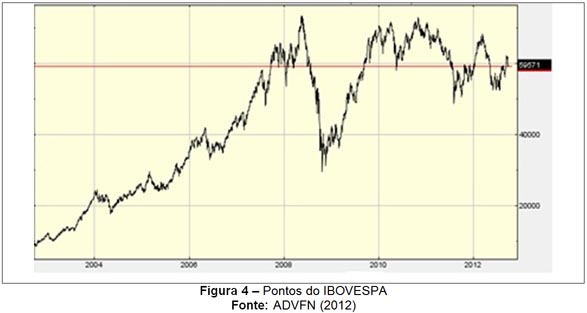
Posteriormente à elaboração das linhas de Fibonacci em Microsoft Excel e análise das ondas, os períodos foram identificados conforme o Quadro 1.

 

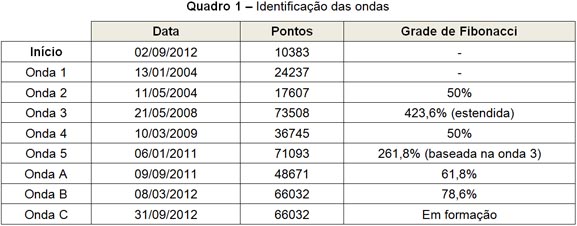
5.2 Escolha de parâmetros

Para escolha do parâmetro a ser simulado, optou-se por aplicar a correlação de Pearson entre os dados utilizando a função correlação da análise de dados do Microsoft Excel, conforme exibe o Quadro 2.

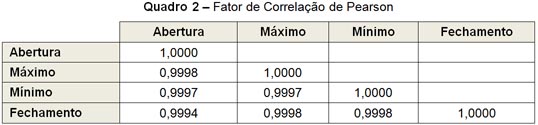
Uma observação do quadro revela que os parâmetros analisados apresentam forte correlação entre si, podendo-se utilizar qualquer um para Simulação de Monte Carlo, em vista da obtenção de resultados muito próximos. Desse modo, optou-se pelos pontos de abertura do IBOVESPA.

 

5.3 Obtenção da FDP

Para se determinar a Função de Densidade Probabilística (FDP), recorreu-se à ferramenta Data Analysis do Crystal Ball da Oracle, na qual são inseridas as séries históricas e se obtêm, como output, o histograma e a função de probabilidade que mais bem representa o histograma. Esse software ao fazer a escolha da função de probabilidades, também executa os testes de Anderson-Darlin, Kolmogorov-Smirnov e Chi-Square para analisar qual distribuição de probabilidades tem melhor aderência em cada situação. Assim, as seguintes funções de probabilidades foram determinadas: para as ondas 2 e 3, respectivamente, a distribuição logística e a distribuição triangular; já para a onda 4, a distribuição Log-Normal; e, para onda 5, a distribuição de Eventos Extremos Mínimos (Min Extreme). Finalmente, as ondas A e B assumiram, respectivamente, a distribuição do tipo Weibull e a distribuição do tipo Eventos Extremos Máximo (Max Extreme).

 

6 Discussão da simulação e dos aspectos econômicos/matemáticos

 

6.1 Simulação da onda 1

Posteriormente a uma tendência de baixa devido à “Bolha Econômica de 2008”, é compreensível que o sentimento dominante no mercado seja o medo. Porém, mesmo após o “esgotamento das forças de baixa”, surgiu um tímido movimento de alta que é imediatamente classificado pela “massa de investidores” como uma simples correção do período de baixa anterior. Alguma abundância de venda de ações a descoberto está em evidência, pois a maioria dos investidores está convencida de que a tendência geral é de baixa. Finalmente, os investidores decidem fazer mais uma “corrida para as vendas", persistindo, entretanto, o pressentimento de que novas baixas virão – habitualmente, esta costuma ser a de menor dimensão quando comparada ao movimento geral de 5 ondas. Por isso, a onda 1 é raramente evidente e é difícil de dimensionar em seu início.

Assim, quando a onda 1 se inicia, a notícia em evidência é quase sempre negativa, como por exemplo, o índice da taxa de desemprego ou o relatório dos novos pedidos de seguro-desemprego nos Estados Unidos da América ou a decisão sobre a taxa de juros do Banco Central Europeu não são bons indicadores. Os analistas fundamentalistas continuam revendo suas estimativas de lucros menores para as empresas e os indicadores macroeconômicos das principais economias não mostram mudanças estruturais significativas.

Com essa tendência, as ações têm movimentos para cima e para baixo na forma de um ziguezague, causados, normalmente, por um número relativamente pequeno de pessoas que, repentinamente, devido a razões reais ou imaginárias, consideram que o preço das ações está baixo, representando um momento perfeito de compra – isso faz com que o preço das ações suba.

 

6.2 Simulação da onda 2

A simulação de Monte Carlo começa pela onda 2, pois a onda 1 serve de base para identificação das demais – a onda 2 inicia em 24.237 pontos e se apresenta três possibilidades conforme a sequência de Fibonacci, ou seja, 50%, 61,8% e 78,6% que representam os pontos 17.310, 15.674 e 13.348, respectivamente. Com a utilização do Crystal Ball para 100.000 rodadas de simulações, obtém-se, de acordo com a Figura 5, as seguintes probabilidades para a simulação da onda 2: 80,1% de chances de atingir até 17.310 pontos, 2,4% de chegar a 15.674 pontos e 1,0% de alcançar 13.348 pontos.

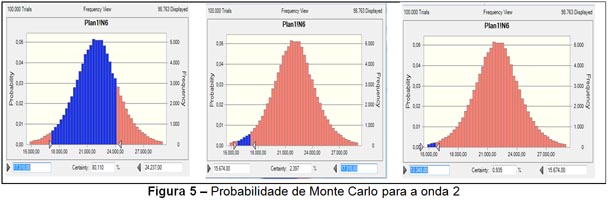
A onda 2 praticamente corrige a onda 1, mas o limite inferior nunca ultrapassa o ponto de partida da onda 1, pois frequentemente apresenta níveis de retração da sequência de Fibonacci. Normalmente, as notícias externas ao mercado financeiro ainda são ruins e um número suficiente de pessoas que estavam na onda original considera a ação supervalorizada e vende seus papéis com a finalidade de obter lucros, fazendo com que o valor das ações caia um pouco.

Os sentimentos em relação ao mercado de baixa estão muito visíveis e claros nos investidores e a sensação de novas mínimas toma conta do mercado. Entretanto, alguns sinais positivos aparecem, mostrando que o volume dos negócios é menor na onda 2 do que na onda 1 e os preços não costumam recuar mais de 61,8% do ganho na onda 1 – além disso, os preços devem cair em um padrão de três ondas.

A onda 2 costuma devolver boa parte dos ganhos da onda 1, sendo que a grande maioria dos investidores ainda acredita na ideia de continuidade da baixa e, nesse clima, alguns investidores começam a comprar e montar suas carteiras. A grande característica da onda 2 é a surpresa, uma vez que o seu fundo sustenta-se acima do fundo da onda 1, quebrando, dessa forme, as expectativas de baixa no valor das ações.

 

6.3 Simulação da onda 3

A onda 3 se inicia com 17.607 pontos, portanto, com três possibilidades de ocorrer de acordo com Fibonacci, ou seja, 161,8%, 261,8% e 463,6% que representam os pontos 40.023, 53.877 e 76.293, respectivamente. Com a utilização do Crystal Ball para simular 100.000 rodadas, conforme o mostrado na Figura 6, obtêm-se, para a onda 3, as probabilidades de 41% de atingir até 40.023 pontos, 38,6% de alcançar 53.877 pontos e 20,3% de chegar a 76.293 pontos.

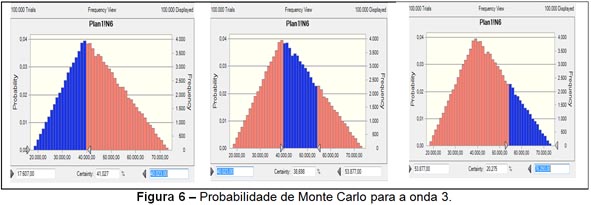
Normalmente, a onda 3 é a maior e apresenta uma grande força dentro dessa tendência, pois se apresenta de “forma mais longa, aguda e prolongada”. O valor das ações chama a atenção do grande público e muitas pessoas decidem entrar no mercado e comprar títulos, fazendo com que o preço deles aumente. A onda 3 ultrapassa o pico criado entre as ondas 1 e 2, pois as notícias agora são mais positivas e as estimativas de lucro mais elevadas – a consequência imediata é a rápida subida de preços, As correções são superficiais e de curta duração. Assim que a onda 3 é iniciada, as notícias ainda indicam baixas, e a maioria dos investidores e especuladores permanece com desconfianças.

Em resumo, nessa onda surge o que se poderia denominar de “efeito manada”, que representa um movimento positivamente correlacionado entre os investimentos, sendo que a partir da sustentação apresentada pelo fundo da onda 2, os investidores passam a ficar otimistas quanto aos fundamentos e passam a operar fortemente na compra, forçando uma rápida alta nos preços das ações – a onda 3 habitualmente é a mais longa, consistente e dinâmica nos mercados à vista.

 

6.4 Simulação da onda 4

Para a onda 4, com início em 73.508 pontos, tem-se quatro probabilidades de acordo com a sequência de Fibonacci: 23,6%, 30%, 38,2% e 50%, que representam os pontos 60.315, 56.738, 52.154 e 45.558, respectivamente. A simulação no Crystal Ball para 100.000 rodadas, exibida nas Figuras 7 e 8, mostra as probabilidades de 10,3% de atingir 60.315 pontos, 5,8% de se alcançar 56.738 pontos, 10,2% de chegar a 52.154 e 21.3% de se obter 45.558 pontos.

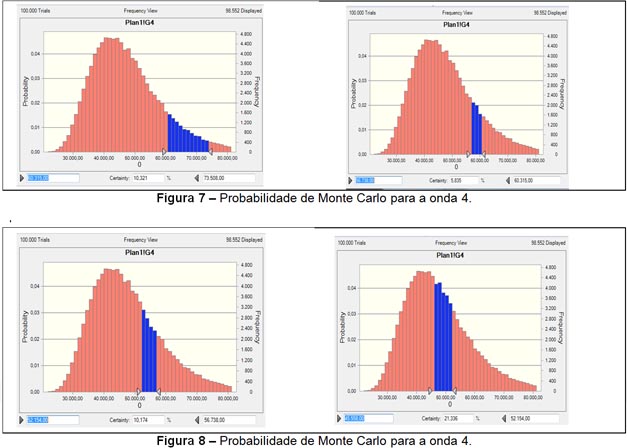
A onda 4 é claramente uma correção e segue os níveis de retração da sequência de Fibonacci, sendo previsível tanto em profundidade como em forma, pois, por alternância com a onda 2, deve diferir em grau. As ações atrasadas que possuíam preços elevados começam a declinar durante a onda 4, onde essa deterioração prepara no mercado um cenário com sinais sutis de fraqueza durante a onda 5. Os preços se movimentam por um período prolongado e, normalmente, são corrigidos na faixa de 23,60% a 50% da sequência de Fibonacci dos ganhos adquiridos na onda 3. No entanto, as estatísticas indicam que a retração, de um modo geral, ocorre na faixa de 30% a 50% do ganho da onda 3. Como mencionado anteriormente, esta onda surge como correção da onda 3. Devido à regra de alternância, caso a onda 2 seja simples (composta por somente uma subonda), a onda 4 deverá ser complexa (subdivididas em ondas A, B e C). Caso a onda 2 seja a mais complexa, então a onda 4 será a mais simples. O comportamento da onda 4 deixa claro que o mercado está em um momento de tomada de fôlego para a continuidade da alta.

 

6.5 Simulação da onda 5

A onda 5 tem início em 36.745 pontos e, como a onda 3 é mais estendida, obtém-se três probabilidades de acordo com a sequência de Fibonacci – 100%, 161,8% e 261,8%, que representam os pontos 50.599, 59.161 e 73.015, respectivamente. Com a simulação no aplicativo Crystal Ball para 100.000 rodadas, chega-se às probabilidades de 19,3% de se atingir 50.599 pontos, 25,2% de alcançar 59.161 pontos e 42,7% de se obter 73.015 pontos, conforme exibe a Figura 9.

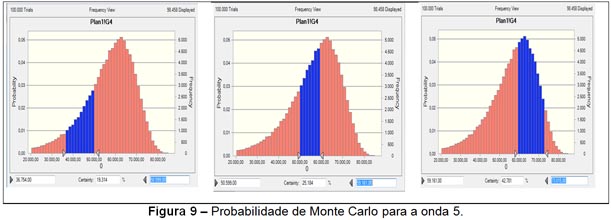
Finalizando-se a onda corretiva 4, ocorre uma “nova arrancada de altas” e os indicadores atingem níveis máximos de rentabilidade – a onda 5 é menos dinâmica do que as três ondas imediatamente anteriores em termos de comprimento, mostrando um ritmo mais lento na variação dos preços dos títulos. Assim, a onda 5 pode ser considerada a etapa final na direção da tendência dominante e, frequentemente, vai além ou "passa pela" onda 3 paralela a uma onda de tendência, conectando o início das ondas 3 e 5. As notícias ainda são positivas e todos estão muito otimistas, sendo que o volume de negociação vai caindo em relação à onda 3, e os indicadores momentâneos começam a apresentar divergências – assim é iniciado o padrão de ondas ABC.

 

6.6 Simulação da onda A

Para a onda A, que teve início em 71.093 pontos, tem-se três possibilidades conforme a sequência de Fibonacci – 50%, 61,8% e 78,6%, que representam os pontos 53.919, 49.866 e 44.095, respectivamente. Com 100.000 rodadas no Crystal Ball, como exibido na Figura 10, são obtidas as probabilidades para a onda A de 76% de se atingir 53.919 pontos, 8,2% de se obter chegar 49.866 pontos e 1,6% de chegar a 44.095 pontos.

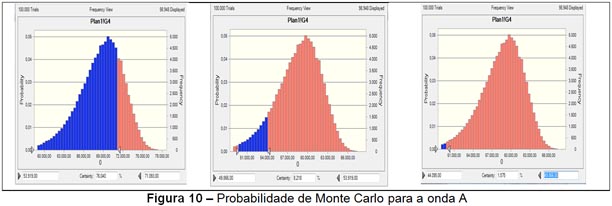
No geral, as correções são mais difíceis de serem identificadas do que os movimentos de impulso – considera-se que na onda A de um mercado em baixa, as notícias externas predominantes ainda são positivas, semelhante à onda 2 (que pode ser entendida como uma onda de retração), sendo de difícil identificação em vista de que suas primeiras manifestações tendem a confundir com uma leve retração que, em seguida, prossegue com a tendência que estava se desenvolvendo. Normalmente, há as seguintes retrações em função da onda 5, segundo a sequência de Fibonacci: 50,00%, 61,80% e 78,60%.No entanto, quando a onda 5 é estendida, as retrações vão de 100% até 178,60% e, em períodos de crise econômica, pode haver uma retração de 261,80% da onda de origem, subdividindo-se em cinco ondas menores.

 

6.7 Simulação da onda B

A onda B inicia em 48.671 pontos, obtendo-se três probabilidades de acordo com a sequência de Fibonacci – 38,2%, 61,8% e 78,6 – que representam os pontos 57.236, 62.528 e 66.295, respectivamente. Com a simulação com o aplicativo Crystal Ball para 100.000 rodadas, conforme mostra a Figura 11, são obtidas as probabilidades de 25,8% de atingir 57.236 pontos, 18,8% de se chegar a 62.528 pontos e 11,9% de alcançar 66.295 pontos.

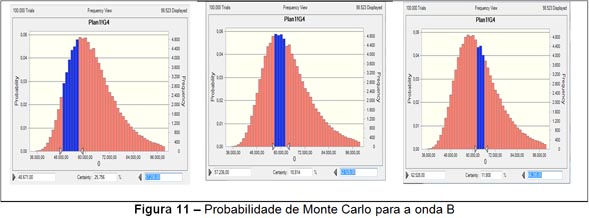
Novamente, com a queda de valor dos títulos relacionados à onda A, os investidores menos experientes (e, portanto, mais otimistas) retomam as compras, mas a significativa redução do volume desta “suposta alta de mercado” abrevia sua duração, constituindo-se em um ótimo ponto de venda.

 

6.8 Simulação da onda C

Os preços das ações se movem impulsionados para baixo em cinco ondas, sendo que o volume aumenta na “terceira perna da onda C”, onde os investidores percebem que o mercado está em baixa – desse modo, as projeções se deterioram desde que o início da onda 1. O mercado de investimentos esperou que os índices de desempenho das principais economias globais reagissem de um período para outro, o que não foi concretizado. Finalmente, observa-se que os dados de desempenho industrial e o aguardado “momento da virada” está ficando para trás. A onda C é normalmente do mesmo tamanho da onda A ou, em muitas vezes, uma relação de 1,618 maior que essa onda. Assim, na onda C, as economias globais se tornam um pouco mais competitivas, apresentando uma série de índices estruturais positivos, que dizem respeito à implementação de medidas estruturais.

Assim, a queda dos mercados não deixa mais dúvidas e, com isso, os investidores profissionais se retiram do mercado ou passam a vender suas posições a qualquer preço, forçando uma queda mais acentuada das cotações e completando um ciclo de oito ondas.

 

Considerações Finais

Conforme os objetivos estabelecidos, conclui-se que o trabalho possibilitou o desenvolvimento de um modelo eficaz de simulação pelo método de Monte Carlo e que, ao mesmo tempo, explicou o comportamento do investidor do ponto de vista econômico e psicológico envolvido em cada período representado pelas ondas analisadas.

O presente estudo possui relevância no sentido de se compreender os problemas e desafios encontrados ao se aplicar a teoria relativa às ondas de Elliott e, também, como uma tentativa de se garantir que as decisões a esse respeito sejam tomadas com maior grau de confiabilidade.

Observou-se que o método de Monte Carlo se constitui em uma excelente ferramenta para aplicação conjunta ao princípio de Elliott, pois permitiu ao analista verificar o percentual de Fibonacci que possui maior probabilidade de ocorrência e, com isso, entender melhor o comportamento do mercado financeiro.

 

REFERÊNCIAS

ANDREZO, A.; LIMA, I.S. Mercado financeiro: aspectos conceituais e históricos. 3.ed. Porto Alegre: Artmed, 2004.

BELMONT, D. F. S. Teoria das ondas de Elliott: uma aplicação ao mercado de ações da BM&F-BOVESPA. João Pessoa, 2010. 78 f. Dissertação (Mestrado em Economia) – Programa de Pós-Graduação em Economia, Universidade Federal da Paraíba.

BM&F BOVESPA/BOLSA DE VALORES DE SÃO PAULO. Mercado – índices. Disponível em: http://www.bovespa.com.br. Acesso em: 18 jun. 2012.

BM&F BOVESPA/BOLSA DE VALORES DE SÃO PAULO. O mercado de capitais: sua importância para o desenvolvimento e os entraves com que se defronta no Brasil. Tendências – Consultoria Integrada. Disponível em: http://www.bovespa.com.br. Acesso em: 29 jan. 2011.

CALAÇA, R. W. Detecção automática de ondas de Elliott em mercado acionário. Goiânia, 2008. 77 f. Dissertação (Mestrado em Engenharia de Elétrica) – Programa de Pós-Graduação em Engenharia Elétrica e Computação, Universidade Federal de Goiás.

ELLIOTT WAVE PREDICTIONS. Elliott wave analysis of GDX. http://elliottwavepredictions.com/ Disponível em: http://elliottwavepredictions.com. Acesso em: 29 jan. 2012.

FERREIRA, J. K. F. S.; SILVA, R. F. M.; GUILHERME, H. F. Um panorama evolutivo das finanças e a aplicação das finanças comportamentais na análise de tomada de decisão dos investidores no mercado de capitais. In: SEMINÁRIO DE CIÊNCIAS CONTÁBEIS, 3., 2003, Recife. Anais... Recife: Universidade Federal de Pernambuco/UFPE, 2003, 15p.

HAYASHI, A. D. Aplicação dos fractais ao mercado de capitais utilizando-se as Elliott waves. Florianópolis, 2002. 121 f. Dissertação (Mestrado em Engenharia de Produção) – Programa de Pós-Graduação em Engenharia de Produção, Universidade Federal de Santa Catarina.

PRECHTER JR., R. R.; FROST, A. J. O princípio da onda de Elliott. Rio de Janeiro: Livros Técnicos e Científicos, 2004.

SILVA, W. F. Contribuição da simulação de Monte Carlo na projeção de cenários para gestão de custos na área de laticínios. Itajubá, 2004. 138 f. Dissertação (Mestrado em Engenharia de Produção) – Programa de Pós-Graduação em Engenharia de Produção, Universidade Federal de Itajubá.

VARGAS, R.V. Construindo previsões de custo final do projeto utilizando análise de valor agregado e simulação de Monte Carlo. Revista Brasileira de Gerenciamento de Projetos, Curitiba, 2004, 16p. Disponível em: http://pm21.com.br/website/index.php?pg=revista&id= 18&id_revista=2. Acesso em: 18 jun. 2012.

 

Recebido em 08/10/2013
Aceito em 10/02/2014

 

---

Revista Científica On-line Tecnologia – Gestão – Humanismo - ISSN: 2238-5819
Faculdade de Tecnologia de Guaratinguetá
Revista v.3, n.1 – maio, 2014